什么是网格分割算法，常见网格分割算法介绍

网格分割算法是一种用于将三维网格模型分解为更小、更有意义的子网格或区域的算法，广泛应用于计算机图形学、三维建模、几何处理和图像处理等领域。网格分割算法的核心目标是根据几何特征、拓扑结构或用户意图将网格分割成有意义的部分，以支持后续的分析、处理和应用。

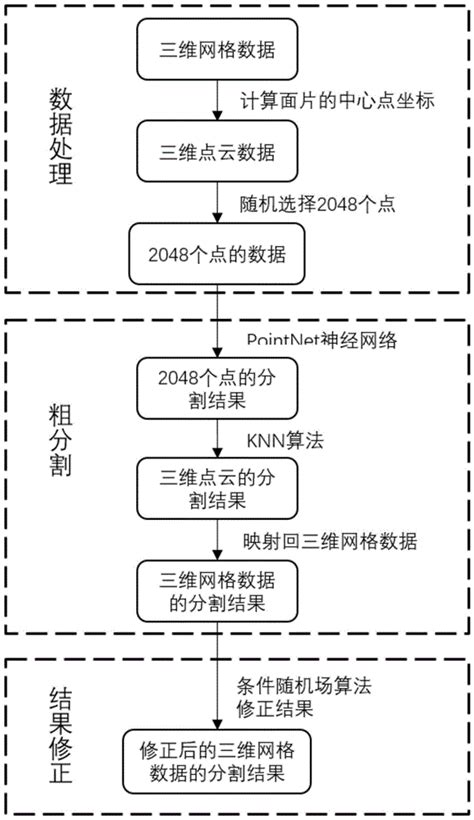
网格分割算法的常见类型和方法

1. 基于聚类的算法
   基于聚类的算法通过将网格中的顶点或面片根据其几何特征（如测地距离、曲率、法向量等）进行聚类，从而实现分割。例如，K-means聚类、谱聚类（Spectral Clustering）等方法被广泛应用于网格分割中。谱聚类算法通过计算拉普拉斯矩阵的特征向量来实现网格分割，能够有效捕捉网格的几何结构信息。
2. 基于层次化分割的算法
   层次化分割算法通过迭代地将网格分割成更小的子部分，通常结合模糊聚类和最小割方法，以实现更精细的分割。例如，Katz等人提出的层次化网格分割算法能够避免过度分割和锯齿形边界。
3. 基于图论和图割的算法
   图论方法在网格分割中也扮演重要角色，例如基于图割（Graph Cut）的算法通过最小化能量函数来实现分割，能够有效处理分割边界和区域的平滑性问题。
4. 基于深度学习的算法
   随着深度学习的发展，基于深度学习的网格分割方法逐渐兴起。这些方法通过端到端的训练，能够自动学习网格的特征表示，并直接进行分割。例如，MeshCNN等网络结构将网格边类比为图像像素，定义卷积和池化操作，以实现网格分割。
5. 基于几何特征的算法
   基于几何特征的算法通过计算网格的几何属性（如曲率、测地距离、体半径等）来指导分割。例如，体半径函数（Volumetric Radius Function）通过测量局部对象的直径，能够有效分割网格。
6. 基于迭代和优化的算法
   一些算法通过迭代优化方法（如最小化能量函数）来实现分割，例如基于水平集（Level Set）的方法通过动态调整分割边界来实现更精确的分割。

网格分割算法的应用领域

网格分割算法在多个领域有广泛应用，包括：

• 三维建模与动画：用于网格参数化、纹理映射、变形等。
• 计算机视觉与图像处理：用于图像分割、目标识别、图像分割等。
• 医学图像处理：用于医学图像的分割和分析。
• 工业设计与制造：用于产品设计、逆向工程、质量检测等。

网格分割算法的挑战与发展趋势

尽管网格分割算法已经取得了显著进展，但仍面临一些挑战，如：

• 分割质量与边界平滑性：如何在保持分割精度的同时实现更平滑的边界。
• 计算效率与实时性：如何在大规模数据下提高计算效率。
• 多尺度与多尺度分割：如何处理不同尺度和复杂度的分割需求。
• 跨领域应用的通用性：如何开发适用于不同应用场景的通用算法。

未来，随着深度学习、多核学习和自适应算法的发展，网格分割算法有望在精度、效率和通用性方面取得进一步突破。

网格分割算法是一种重要的三维几何处理技术，通过多种方法实现网格的分割，广泛应用于多个领域。随着算法的不断发展，其在复杂场景下的应用前景将更加广阔。