Z字形编码(Zigzag Coding)是一种在图像和数据压缩中广泛应用的技术,尤其在JPEG图像压缩中扮演着关键角色。它主要用于重新排列二维矩阵中的系数,以提高后续压缩效率。
1. 基本原理
Z字形编码的核心思想是将二维矩阵中的系数按照Z字形的顺序重新排列成一维序列。这种排列方式能够将低频系数(通常集中在矩阵的左上角)放在序列的开头,而高频系数则位于序列的末尾。这种排列方式有助于后续的压缩算法(如行程长度编码)更高效地处理数据。
2. 在JPEG压缩中的应用
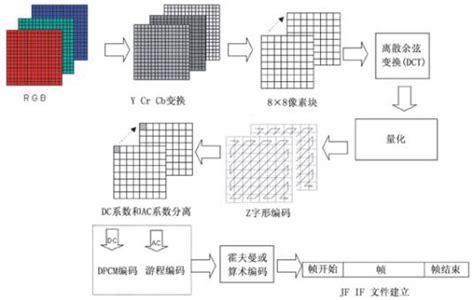
在JPEG压缩中,Z字形编码是DCT(离散余弦变换)后处理的重要步骤。DCT将图像转换为频率域,其中低频系数(低频)集中在左上角,高频系数则分布在右下角。Z字形编码将这些系数重新排列成一维序列,使得连续的“0”系数(即“0”的行程长度)增加,从而为后续的行程长度编码(RLE)和熵编码(如Huffman编码)提供更好的压缩基础。
3. Z字形编码的实现
Z字形编码的实现通常涉及将二维矩阵(如8×8的DCT系数矩阵)按照Z字形的路径遍历,将每个元素依次放入一维数组中。例如,从左上角开始,向右下角移动,然后向上移动,再向右下角移动,如此往复,直到遍历整个矩阵。
4. Z字形编码的优势
- 提高压缩效率:Z字形编码通过将低频系数集中排列,使得后续的行程长度编码(RLE)能够更有效地压缩数据。由于低频系数通常较小,连续的“0”系数较多,因此可以显著减少数据量。
- 提高压缩效率:Z字形编码为后续的熵编码(如Huffman编码)提供了更好的输入,因为一维序列更容易进行编码。
5. Z字形编码的其他应用
除了在图像压缩中的应用,Z字形编码也被用于其他领域,如图像处理、数据压缩和信号处理等。例如,在图像处理中,Z字形扫描(Zigzag Scan)是一种常见的图像扫描方式,用于将二维图像数据转换为一维序列。
6. Z字形编码的变体
虽然Z字形编码在图像压缩中应用广泛,但也有其他类似的编码方式,如Z编码(Z-Encoding)和Z-Code(国际疾病分类中的代码),这些术语在不同领域有不同的含义。
总结
Z字形编码是一种在图像和数据压缩中广泛应用的技术,通过将二维矩阵中的系数重新排列为一维序列,以提高压缩效率。它在JPEG压缩中扮演着关键角色,通过将低频系数集中排列,为后续的压缩算法提供了更好的输入。

