什么是Radon变换

Radon变换是一种数学变换，广泛应用于图像处理、医学成像、计算机视觉等领域。它通过将二维图像在不同角度上的投影信息提取出来，从而实现图像的重建和分析。

1. 定义与基本概念

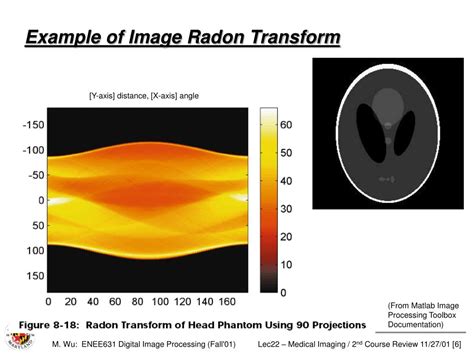
Radon变换是一种数学积分变换，其核心思想是将二维图像中的信息转换为一维投影数据。具体来说，Radon变换将二维图像中的每个点沿不同方向的投影值进行积分，从而生成一组投影数据。这些投影数据包含了原始图像的几何结构和特征信息。

3. 几何解释

从几何角度看，Radon变换可以理解为将图像中的每个点沿不同方向的投影线进行积分。例如，对于图像中的每个点，沿不同方向的投影线会穿过该点，从而生成投影值。这些投影值可以用于重建图像的结构和特征。

4. 应用领域

Radon变换在多个领域有广泛应用，包括：

• 医学成像：在CT（计算机断层扫描）中，Radon变换用于从多个角度的投影数据重建图像，从而实现非侵入式成像。
• 图像处理：Radon变换可用于图像增强、特征提取和图像重建等任务。
• 工业检测：在无损检测中，Radon变换可用于分析材料内部结构。

5. 逆变换与重建

Radon变换的逆变换（逆Radon变换）可以将投影数据重建为原始图像。通过傅里叶变换和傅里叶切片定理，可以将Radon变换与傅里叶变换联系起来，从而实现图像的重建。在实际应用中，通过增加投影数量和使用滤波器，可以提高重建图像的质量。

6. 实现与工具

在实际应用中，Radon变换可以通过多种编程语言和工具实现。例如，MATLAB和Python提供了Radon变换和逆Radon变换的函数，如radon和iradon，用于图像处理和图像重建。

7. 挑战与改进

尽管Radon变换在图像重建和分析中具有重要应用，但也面临一些挑战，如投影数据的不完备性、重建精度的提高等问题。通过改进算法和引入正则化方法，可以进一步提高重建效果。

总结

Radon变换是一种强大的数学工具，广泛应用于图像处理、医学成像和计算机视觉等领域。通过将二维图像转换为一维投影数据，Radon变换为图像的重建和分析提供了理论基础和技术支持。