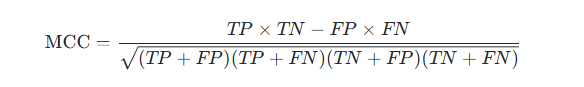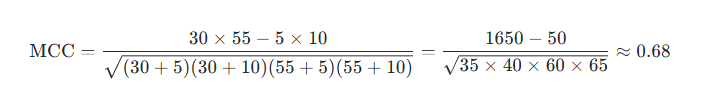什么是Matthews Correlation Coefficient（MCC）

Matthews Correlation Coefficient（MCC）概述

Matthews Correlation Coefficient（MCC），又称马修斯相关系数，是一种用于评估二元（或多类）分类模型性能的统计指标。它通过同时考虑 真正例（TP）‍、真负例（TN）‍、假正例（FP）‍、假负例（FN）‍ 四个混淆矩阵元素，给出一个在 ‑1 到 +1 之间的数值，能够客观反映预测与真实标签之间的相关程度。

1. 计算公式

当分母中任意一项为 0 时，常将分母设为 1，使 MCC 为 0（即等价于随机预测）。

2. 取值意义

取值范围	含义
+1	完全正相关，模型预测与真实标签完全一致（完美预测）
0	无相关性，模型表现相当于随机猜测
‑1	完全负相关，模型预测与真实标签完全相反（完全错误）

3. 为什么使用 MCC？

平衡性：MCC 同时考虑四种分类结果，避免了仅使用准确率（Accuracy）在类别不平衡时产生的误导。即使正负样本比例悬殊，MCC 仍能提供可靠的评估。
对称性：交换正负类标签后，MCC 值不变，体现了指标的对称特性。
与其他指标的关系：MCC 等价于 Pearson 相关系数 在二元分类情形下的形式，也可视为 几何平均的 informedness 与 markedness。

4. 适用场景

类别极度不平衡 的二元分类任务（如疾病筛查、欺诈检测）。
需要 综合评估 正负类预测质量的场景。
多类分类的扩展（通过“一对多”或“一对一”方式计算每对类别的 MCC，再取平均）。

5. 示例计算（便于理解）

假设某模型在 100 条样本上的混淆矩阵如下：

	预测正例	预测负例
实际正例	TP = 30	FN = 10
实际负例	FP = 5	TN = 55

代入公式：

该值接近 1，说明模型在正负两类上均表现良好。

6. 局限与注意事项

分母为零：当任意一项（如 TP+FP）为 0 时，MCC 公式不可直接计算，需要手动设为 0 或使用平滑处理。
解释难度：相较于准确率、召回率等直观指标，MCC 的数值解释对非专业人士可能不够直观，需要配合解释说明。
多类扩展：直接在多类情形下使用 MCC 需要先将问题转化为二元形式，否则可能失去部分信息。

7. 与其他常用指标的对比（简要）

指标	关注点	对类别不平衡的鲁棒性
Accuracy	正确率	低（易被多数类主导）
Precision / Recall	正例预测质量	中等（单独关注正例）
F1‑Score	Precision 与 Recall 的调和均值	中等
MCC	四类混淆矩阵整体平衡	高（最全面）

总结
Matthews Correlation Coefficient 是一种兼顾 平衡性、对称性 与 统计严谨性 的分类评估指标，尤其适用于 类别不平衡 的二元或多类任务。通过其取值范围（‑1~+1）可以直观判断模型的预测质量，是机器学习与统计分析中重要的性能度量之一。

参考: