什么是FP32（单精度浮点数）

1. 定义与结构

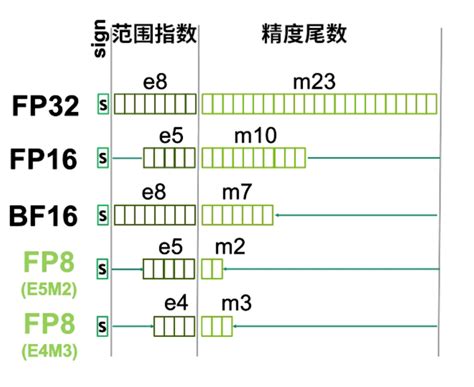
FP32（单精度浮点数）是一种32位（4字节）的浮点数格式，遵循IEEE 754标准。它由以下部分组成：

• 1位符号位（Sign bit） ：表示数值的正负（0表示正数，1表示负数）。
• 8位指数位（Exponent bit） ：用于表示数值的范围（指数部分）。
• 23位尾数位（Mantissa bit） ：用于表示数值的精度（小数部分）。

这种结构使得FP32能够在有限的位数内表示一个范围较大的数值，同时保持一定的精度。

2. 数值范围与精度

FP32的数值范围大约为 1.18 × 10⁻³⁸ 到 3.40 × 10³⁸，其有效数字精度约为 6到9位。这意味着FP32能够表示的数值范围较大，但精度相对较低，适合对精度要求不高的场景。

3. 应用场景

FP32广泛应用于以下领域：

• 深度学习与机器学习：FP32是深度学习训练和推理的基准格式，许多模型训练和推理任务都使用FP32作为默认精度。
• 图形处理：在GPU中，FP32常用于图形渲染和计算，其计算速度和内存占用相对较低。
• 科学计算：在一些对精度要求较高的科学计算中，FP32也被使用，但通常会结合其他精度更高的格式（如FP64）使用。

4. 与其他浮点数格式的比较

• FP16（半精度浮点数） ：FP16使用16位（2字节）表示，精度和范围均低于FP32，但计算速度更快，常用于加速计算。
• FP64（双精度浮点数） ：FP64使用64位（8字节）表示，精度更高，但计算和存储开销更大，通常用于高精度科学计算。
• TF32（NVIDIA提出的格式） ：TF32是一种介于FP32和FP16之间的格式，精度略低于FP32，但计算效率更高，适用于AI训练。

5. 性能与计算效率

FP32的计算效率较高，尤其是在GPU等硬件加速设备上，FP32的计算速度通常以TFLOPS（万亿次浮点运算每秒）为单位衡量。例如，高端GPU的FP32算力可达数十TFLOPS。

6. 混合精度训练

在深度学习中，FP32常与其他低精度格式（如FP16、BF16）结合使用，形成混合精度训练策略，以在保持模型精度的同时提高计算效率。

总结

FP32（单精度浮点数）是一种广泛应用于计算机科学和工程领域的数据格式，具有较高的计算效率和一定的精度，适用于多种应用场景，包括深度学习、图形处理和科学计算。尽管其精度相对较低，但其在许多实际应用中仍被广泛采用