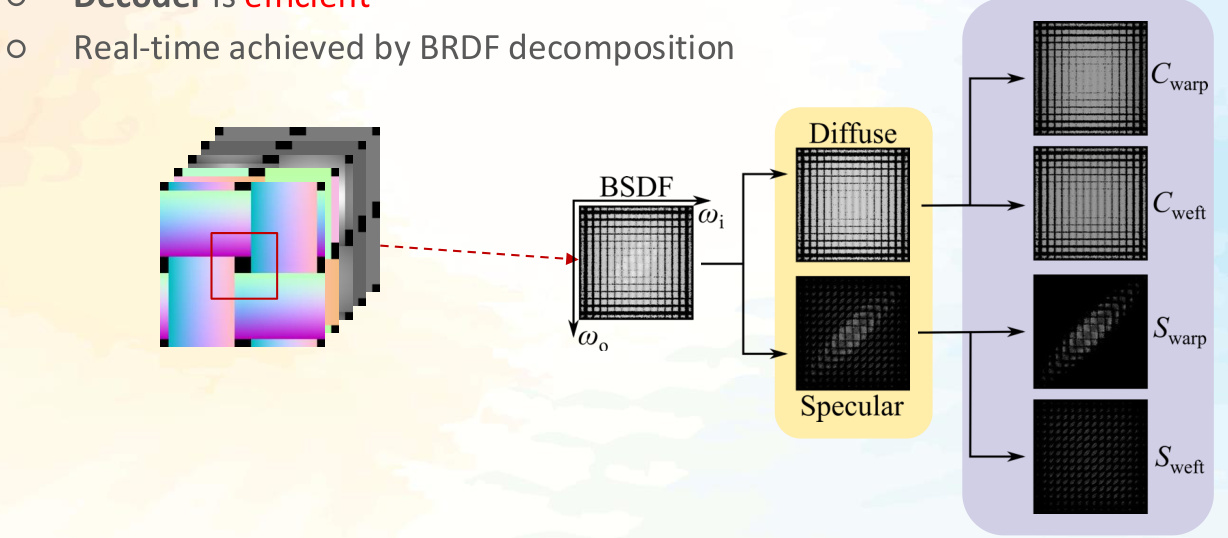
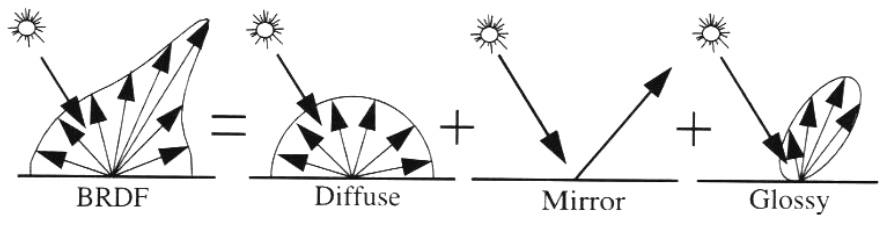
什么是BRDF分解

AI解读 22小时前硕雀

7 0 0

BRDF（Bidirectional Reflectance Distribution Function，双向反射分布函数）是计算机图形学和光学中的一个核心概念，用于描述物体表面如何将入射光反射到特定方向的特性。BRDF 是一个四维函数，其输入包括入射光方向 $v^i$ 、出射光方向 $v^r$ 、表面法线方向 $n^$ ，以及可能的表面参数（如粗糙度、材质属性等），输出则是反射光的强度或辐射度。BRDF 的定义可以表示为：

fr(v^i,v^r,n^)=Le(v^r)Ei(v^i)

其中， $Le(v^r)$ 是出射光的辐射度， $Ei(v^i)$ 是入射光的辐照度。BRDF 描述了在给定入射和出射方向下，表面反射光的分布特性。

BRDF 的分解

BRDF 的分解是指将复杂的四维函数 $fr(v^i,v^r,n^)$ 分解为多个低维函数的乘积或组合，以简化其表示和计算。这种分解方法在计算机图形学中被广泛应用于实时渲染、光照模拟和材料建模等领域。常见的分解方法包括：

1. 2D 分解

Lawrence 等人提出了 BRDF 的 2D 分解方法，将 BRDF 分解为两个方向的函数的乘积。例如，可以将 BRDF 分解为入射方向和出射方向的函数，分别表示为 $G(v^i)$ 和 $F(v^r)$ ，使得：

fr(v^i,v^r,n^)=G(v^i)⋅F(v^r)

这种分解方法可以将四维 BRDF 转换为两个二维函数的乘积，从而简化存储和计算。例如，在 PBR（基于物理的渲染）中，BRDF 可以分解为漫反射（Diffuse）和镜面反射（Specular）两个部分，分别对应不同的反射机制。

2. 1D 分解

除了 2D 分解，还有 1D 分解方法，即将 BRDF 分解为多个一维函数的乘积。例如，可以将 BRDF 分解为入射方向和出射方向的函数，分别表示为 $u (θ_{i})$ 和 $v (θ_{r})$ ，使得：

fr(v^i,v^r,n^)=u(θi)⋅v(θr)

这种分解方法适用于具有方向不变性的 BRDF，例如在某些各向同性表面中，反射特性与入射和出射方向的角度无关。

3. 混合分解

混合分解方法将 BRDF 分解为多个 BRDF 或波瓣的混合。例如，可以将 BRDF 分解为漫反射和镜面反射的混合，表示为：

fr(v^i,v^r,n^)=α⋅fdiffuse(v^i,v^r,n^)+(1−α)⋅fspecular(v^i,v^r,n^)

其中， $α$ 是一个混合系数，表示漫反射和镜面反射的权重。这种分解方法适用于具有复杂反射特性的表面，例如金属和玻璃等材料。

4. 同态分解

同态分解是将 BRDF 分解为多个低维正值因子的乘积，并使用对数变换将其转换为线性数据拟合问题。例如，可以将 BRDF 分解为 $fr(v^i,v^r,n^)=A(v^i)⋅B(v^r)⋅C(n^)$ ，其中 $A$ 、 $B$ 、 $C$ 是低维函数。这种分解方法可以用于近似任意 BRDF，并允许在图形硬件中进行实时渲染。

5. 球谐函数分解

球谐函数（Spherical Harmonics）是一种应用于球面上的傅里叶基函数，可以用于表示 BRDF 的四维空间。球谐函数分解方法将 BRDF 表示为球谐函数的线性组合，从而将四维 BRDF 转换为低维系数，便于存储和计算。例如，可以将 BRDF 分解为：

fr(v^i,v^r,n^)=∑l=0L∑m=−llalm⋅Ylm(v^i)⋅Ylm(v^r)

其中， $Y_{l m}$ 是球谐函数， $a_{l m}$ 是系数。这种分解方法适用于具有方向不变性的 BRDF，并且可以用于实时渲染和光照模拟。

6. 小波分解

小波分解是一种线性算子，可以将函数编码为不同分辨率或尺度下的系数，从而实现压缩。例如，可以将 BRDF 分解为多个小波系数的组合，从而将四维 BRDF 转换为低维系数，便于存储和计算。例如，可以将 BRDF 分解为：

fr(v^i,v^r,n^)=∑k=0Kck⋅ψk(v^i,v^r,n^)

其中， $ψ_{k}$ 是小波函数， $c_{k}$ 是系数。这种分解方法适用于具有方向变化性的 BRDF，并且可以用于实时渲染和光照模拟。

BRDF 分解的应用

BRDF 分解在计算机图形学中有广泛的应用，包括：

实时渲染：通过将 BRDF 分解为低维函数，可以将复杂的四维 BRDF 存储为纹理，并在图形硬件中进行实时渲染。例如，Lambertian 模型和 Cook-Torrance 模型都是基于 BRDF 分解的典型模型。
光照模拟：BRDF 分解可以用于模拟真实世界的光照效果，例如在 PBR 渲染中，BRDF 分解可以用于模拟金属、玻璃和塑料等材料的反射特性。
遥感图像处理：BRDF 分解可以用于提高遥感图像的空间和时间分辨率。例如，基于 NDVI 的 BRDF 分解算法和反射率降尺度 BRDF 分解算法可以用于提高遥感图像的精度和分辨率。
逆渲染：BRDF 分解可以用于逆渲染，即从图像中恢复表面的反射特性。例如，重要性采样 BRDF 分解方法可以用于减少 BRDF 导数的方差，从而改善逆渲染中的纹理恢复。

总结

BRDF 分解是将复杂的四维 BRDF 函数分解为多个低维函数的乘积或组合，以简化其表示和计算。常见的分解方法包括 2D 分解、1D 分解、混合分解、同态分解、球谐函数分解和小波分解。这些分解方法在计算机图形学中有广泛的应用，包括实时渲染、光照模拟、遥感图像处理和逆渲染等。通过 BRDF 分解，可以更高效地模拟真实世界的光照效果，并提高渲染和图像处理的精度和效率

声明：文章均为AI生成，请谨慎辨别信息的真伪和可靠性！