什么是谱聚类（Spectral Clustering）

谱聚类（Spectral Clustering）是一种基于图论和线性代数的聚类算法，广泛应用于数据挖掘、机器学习和模式识别等领域。它能够处理非凸形状、高维数据以及具有复杂结构的数据集，具有较强的鲁棒性和灵活性。

核心原理与方法

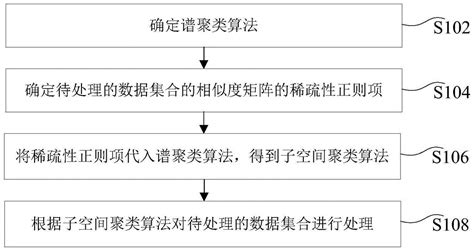
谱聚类的基本思想是将数据点视为图中的节点，节点之间的相似性表示为图中的边。通过构建相似性矩阵（如邻接矩阵或拉普拉斯矩阵），谱聚类将聚类问题转化为图的划分问题，即寻找图的最优划分，使得同一子图内的节点相似度高，而不同子图之间的相似度低。

具体步骤包括：

1. 图表示：将数据点表示为图中的节点，节点之间的相似性（如距离或相似度）表示为边的权重。
2. 相似性矩阵：构建相似性矩阵（如邻接矩阵或拉普拉斯矩阵），用于描述节点之间的关系。
3. 特征分解：对相似性矩阵进行特征分解，得到特征向量和特征值。
4. 降维与聚类：利用特征向量进行降维，然后使用聚类算法（如K-means）对降维后的数据进行聚类。

优势与特点

谱聚类具有以下优势：

• 处理非凸数据：能够处理非凸形状和复杂结构的数据，如图像分割、社交网络分析等。
• 鲁棒性：对噪声和离群点具有较强的鲁棒性。
• 灵活性：适用于高维数据和大规模数据集。

应用领域

谱聚类广泛应用于多个领域，包括：

• 图像分割：用于图像分割和图像处理。
• 社交网络分析：用于社区检测和网络分析。
• 基因组学：用于基因表达数据分析和生物信息学。
• 异常检测：用于检测异常数据点。

缺点与挑战

尽管谱聚类具有诸多优势，但也存在一些缺点：

• 计算复杂度高：需要进行特征分解和特征值计算，计算量较大。
• 参数敏感：聚类效果对相似性矩阵的选择和参数设置较为敏感。
• 可扩展性：在大规模数据集上可能面临性能瓶颈。

实现与工具

谱聚类可以通过多种工具和库实现，如Python中的scikit-learn库提供了SpectralClustering类，支持多种参数配置和聚类方法。

总结

谱聚类是一种基于图论和线性代数的聚类算法，能够有效处理非凸、高维和复杂结构的数据集。它通过构建相似性矩阵和特征分解，将聚类问题转化为图的划分问题，具有较强的鲁棒性和灵活性。尽管存在计算复杂度和参数敏感性等挑战，但其在图像分割、社交网络分析、基因组学等领域的广泛应用使其成为机器学习和数据挖掘中的重要工具