什么是自组织映射（SOM）

自组织映射（Self-Organizing Map, SOM）是一种无监督学习算法，用于将高维数据映射到低维空间，以便进行数据可视化、聚类和降维。该算法由芬兰科学家Teuvo Kohonen于1982年提出。SOM通过神经网络模型，将输入数据映射到二维或一维网格上，同时保持数据的拓扑结构。

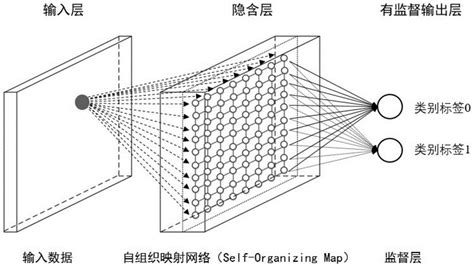
核心原理与工作原理

SOM的核心思想是通过“自组织”能力，使神经元逐渐适应输入数据的特征。其工作原理包括以下几个步骤：

1. 初始化：随机初始化神经元的权重向量，每个神经元对应一个d维向量。
2. 输入数据：将输入数据逐步输入神经网络进行训练。
3. 计算距离：对于每个输入数据，计算其与所有神经元权重向量之间的距离，通常使用欧氏距离。
4. 选择最佳匹配单元（BMU） ：找到最接近输入数据的神经元（获胜神经元）。
5. 更新权重：调整获胜神经元及其邻近神经元的权重向量，使其更接近输入数据。邻域函数（如高斯函数）控制更新范围。
6. 迭代训练：重复上述步骤，直到达到预定的迭代次数或收敛条件。

优势与特点

SOM具有以下优势：

• 无监督学习：无需标签数据，适用于聚类和降维任务。
• 拓扑保形性：能够保持数据的拓扑结构，适合可视化高维数据。
• 自适应性：通过竞争学习机制，神经元能够自适应地调整以适应输入数据。
• 广泛应用：广泛应用于数据挖掘、图像处理、生物信息学、模式识别等领域。

局限性

尽管SOM具有诸多优势，但也存在一些局限性：

• 计算复杂度高：训练过程可能需要大量计算资源。
• 参数敏感：对初始值、学习率、邻域函数等参数敏感，可能影响结果。
• “死神经元”问题：部分神经元可能无法有效更新，导致信息丢失。

应用领域

SOM在多个领域有广泛应用，包括：

• 数据可视化：将高维数据映射到二维空间，便于直观分析。
• 聚类分析：自动发现数据中的模式和结构。
• 图像处理：用于图像分割、特征提取等任务。
• 生物信息学：用于基因表达分析、蛋白质组学等。

实现与工具

SOM的实现通常涉及神经网络模型，可通过编程语言（如Python）实现，MATLAB等工具也提供了相关工具箱。

自组织映射（SOM）是一种强大的无监督学习算法，通过自组织机制将高维数据映射到低维空间，广泛应用于数据可视化、聚类和降维任务。尽管存在一些局限性，但其在多个领域展现出显著的应用价值