什么是算术编码（Arithmetic Coding）

算术编码（Arithmetic Coding）是一种用于数据压缩的熵编码方法，它通过将整个消息编码为一个介于0和1之间的实数，从而实现高效的数据压缩。与霍夫曼编码相比，算术编码能够更精细地利用数据的概率分布信息，因此通常具有更高的压缩比。

核心原理

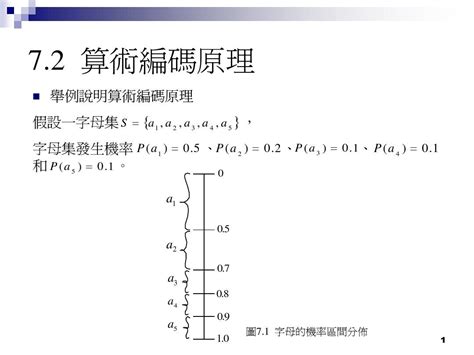
算术编码的核心思想是将整个消息编码为一个介于0和1之间的实数。编码过程通过将符号的概率分布映射到区间内，逐步缩小区间，最终得到一个实数作为编码结果。解码过程则通过反向查找该实数在各个符号概率区间内的位置，逐步还原原始消息。

编码与解码过程

1. 编码过程：
   • 初始区间为[0, 1)。
   • 对于每个符号，根据其概率调整区间，逐步缩小区间范围。
   • 最终得到一个介于0和1之间的实数作为编码结果。
2. 解码过程：
   • 根据编码值在各个符号概率区间内的位置，反推出原始符号。
   • 通过逐步调整区间，逐步还原原始消息。

优势与特点

• 更高的压缩比：算术编码能够更精细地利用数据的概率分布信息，因此通常比霍夫曼编码具有更高的压缩比。
• 适应性强：算术编码能够适应变化的分布，不需要事先计算符号序列的概率。
• 渐近最优：算术编码在理论上接近信息熵的极限，是渐近最优的编码方法。

实现与应用

算术编码在数据压缩领域有广泛应用，例如图像压缩、语音压缩和视频压缩等。例如，MPEG-4标准中使用了算术编码与小波变换结合的图像压缩方法。此外，算术编码在Bzip2和bzip2压缩中也有应用。

挑战与局限性

• 实现复杂性：算术编码的实现相对复杂，需要处理浮点数运算和区间调整等问题。
• 对精度要求高：算术编码需要处理任意精度的实数运算，对精度要求较高。

算术编码是一种高效的数据压缩方法，通过将整个消息编码为一个介于0和1之间的实数，实现了更高的压缩比和更好的适应性。尽管实现复杂，但其在数据压缩领域有广泛应用