什么是离散傅里叶变换（DFT）

离散傅里叶变换（Discrete Fourier Transform，缩写为DFT）是一种将离散时间域信号转换为离散频域信号的数学方法，其核心思想是将有限长度的信号序列分解为不同频率的正弦和余弦波，从而便于分析和处理信号。DFT是傅里叶变换在时域和频域上都呈离散形式的变换，其输入和输出均为有限长序列，视为离散周期信号的主值序列。DFT的定义为对有限长序列进行周期延拓后计算。

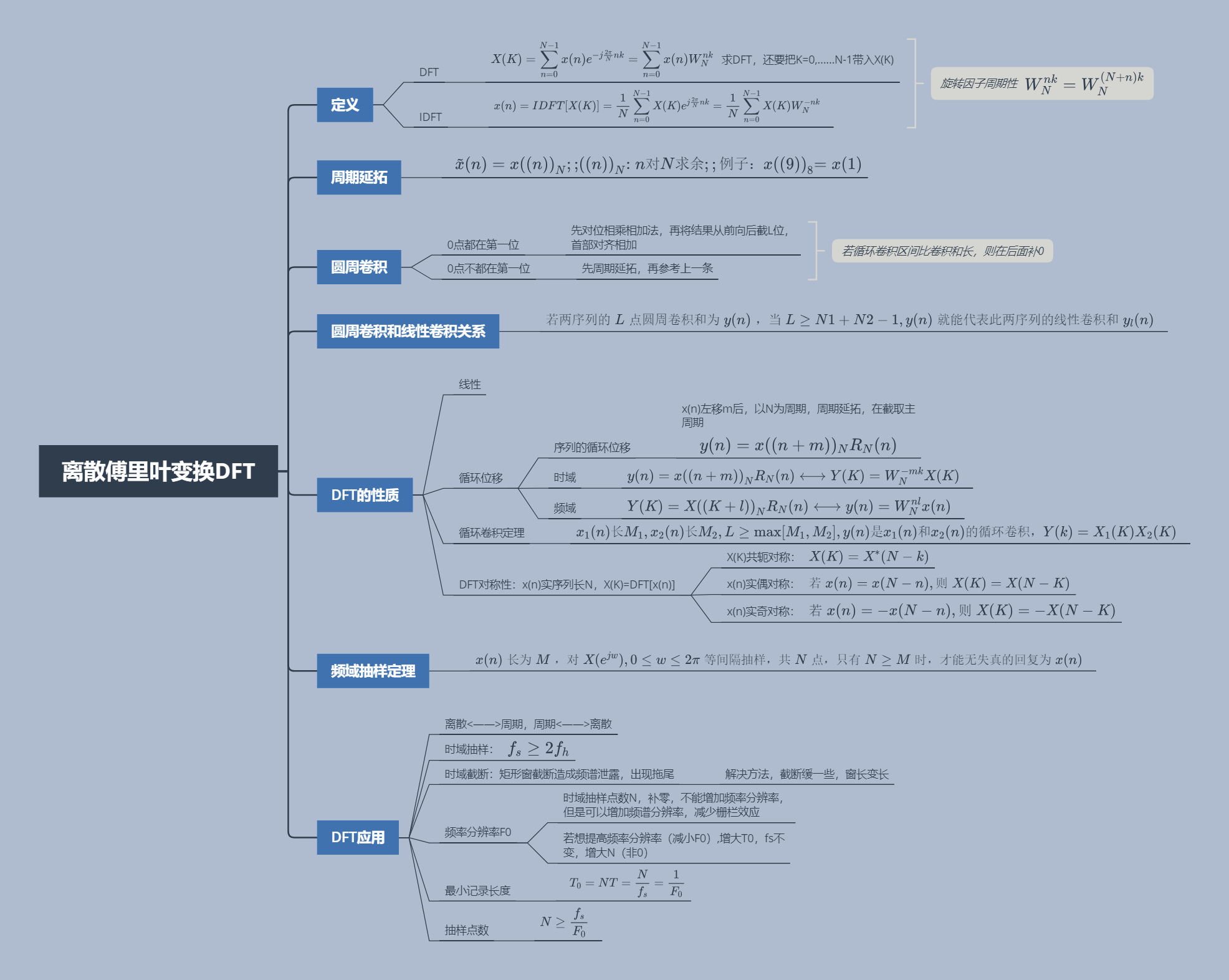
DFT的基本原理是将有限长离散序列从时域转换到频域，其核心是将信号分解为一系列有限的复指数谐波的叠加，从而揭示信号在频域中的特性。DFT能够将有限长离散信号转换为离散频谱，解决了实际计算问题，广泛应用于信号处理、图像处理、通信等领域。例如，在信号处理中，DFT可用于频谱分析、滤波和压缩；在图像处理中，DFT可用于图像增强、压缩和复原。

DFT的计算通常采用快速傅里叶变换（FFT）算法以提高计算效率，FFT是计算DFT或其逆变换的一种高效算法。DFT具有对称性、周期性、线性性等性质，且满足Parseval定理和Plancherel定理，这些性质使其在信号处理和通信系统中具有重要应用。

DFT的定义和性质在多个领域中被广泛应用，包括信号处理、图像处理、通信系统、数据压缩、偏微分方程求解等。DFT的数学基础和应用方法在多个学术论文和教程中被详细阐述，为相关领域的研究和实践提供了理论支持。

离散傅里叶变换（DFT）是一种重要的数学工具，通过将离散时间信号转换为频域信号，为信号分析、处理和应用提供了理论基础和方法支持。