什么是期望最大化（Expectation-Maximization，EM）算法

期望最大化（Expectation-Maximization，EM）算法是一种用于求解最优化问题的迭代算法，尤其适用于含有隐变量的概率模型参数估计问题。EM算法通过交替进行期望步骤（E步）和最大化步骤（M步）来逐步优化模型参数，从而逼近最优解。

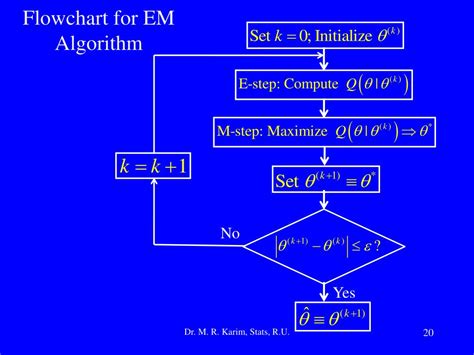
核心思想与步骤

EM算法的核心思想是通过迭代优化来处理含有隐变量（latent variables）或缺失数据的问题。在数据中存在未知类别信息或未观测数据时，直接使用最大似然估计（MLE）可能无法直接求解参数。EM算法通过引入隐变量，并通过迭代优化来逐步逼近最优解。

1. E步（Expectation Step）

在E步中，算法根据当前参数估计值，计算隐变量的期望值。这通常涉及计算给定观测数据的隐变量的后验分布，从而估计隐变量的期望值。例如，在高斯混合模型（GMM）中，E步计算每个数据点属于不同高斯分量的概率。

2. M步（Maximization Step）

在M步中，算法通过最大化E步中计算得到的期望值，更新模型参数。这一步骤通常涉及最大化似然函数或边缘似然函数，以找到新的参数估计值。例如，在高斯混合模型中，M步更新各高斯分量的均值、方差和混合权重。

3. 迭代收敛

EM算法通过重复执行E步和M步，逐步优化参数，直到参数收敛或达到预定的迭代次数。EM算法保证在每次迭代中目标函数（如对数似然函数）不会下降，因此最终收敛到局部最优解。

应用领域

EM算法在多个领域有广泛应用，包括但不限于：

• 机器学习：用于高斯混合模型（GMM）、隐马尔可夫模型（HMM）、主题模型（如LDA）等参数估计。
• 统计学：用于处理缺失数据、不完整数据的分析。
• 计算机视觉：用于图像分割、图像重建等任务。
• 生物信息学：用于基因表达分析、蛋白质结构预测等。

优点与局限性

EM算法的优点包括：

• 适用于含有隐变量或缺失数据的问题；
• 收敛速度快，实现简单；
• 在许多实际应用中表现良好。

然而，EM算法的局限性包括：

• 仅能收敛到局部最优解，无法保证全局最优；
• 对初始参数敏感，可能陷入局部最优解。

总结

期望最大化（EM）算法是一种强大的迭代优化算法，通过交替进行期望步骤和最大化步骤，逐步优化模型参数，广泛应用于概率模型、统计学和机器学习等领域。尽管存在局限性，但其在处理隐变量和缺失数据问题时具有显著优势。