最小角回归(Least Angle Regression, LARS)是一种用于高维数据回归和特征选择的算法,由 Bradley Efron、Trevor Hastie、Iain Johnstone 和 Robert Tibshirani 于 2004 年提出 。该算法旨在解决在特征数量远大于样本数量(p >> n)的情况下,传统回归方法(如最小二乘法)面临的过拟合和不稳定问题 。
算法原理与特点
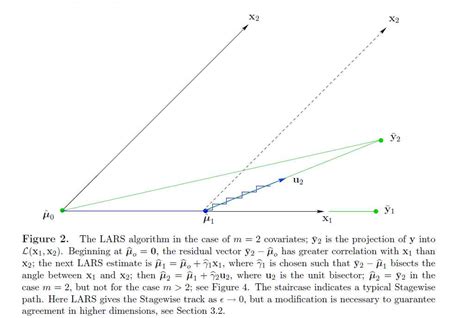
LARS 算法结合了前向选择法和前向梯度法的优点,通过逐步调整变量系数来构建模型。其核心思想是:在每一步中,选择与当前残差方向最相关的变量,并沿该方向调整系数,直到出现新的变量与残差方向相关性相同,此时沿两个变量的角平分线方向调整系数 。这种“最小角”特性使得 LARS 在处理高维数据时具有更高的稳定性和计算效率 。
LARS 算法的主要步骤包括:
- 初始化:从零向量开始,计算残差。
- 选择变量:选择与当前残差方向相关性最大的变量。
- 调整系数:沿该方向调整系数,直到出现新的变量与残差方向相关性相同。
- 重复:重复上述步骤,直到所有变量被选入或残差足够小 。
优点与适用场景
LARS 算法在处理高维数据(p >> n)时表现出色,计算效率高,且计算复杂度与普通最小二乘法(OLS)相同 。它能够有效进行特征选择,生成稀疏模型,并支持 Lasso 回归等变体 。此外,LARS 算法在数值稳定性方面优于传统前向选择法,且在处理噪声数据时表现稳定 。
缺点与局限性
尽管 LARS 算法在高维数据中表现良好,但其对训练集中的噪声敏感,且在某些情况下可能产生不可预测的结果 。此外,LARS 算法的实现和调试可能较为复杂,尤其是在大规模数据集上 。
应用与实现
LARS 算法广泛应用于统计学、机器学习和数据挖掘领域,特别是在高维数据回归、特征选择和模型选择中 。在 Python 中,LARS 算法可通过 scikit-learn 库实现,支持多种参数调整和模型评估 。
总结
最小角回归(LARS)是一种高效、稳定且适用于高维数据的回归算法,通过逐步调整变量系数和残差方向,实现了对复杂数据的建模和特征选择。尽管存在一定的局限性,但其在高维数据处理和稀疏模型构建方面具有显著优势

