什么是最小生成树（MST）

最小生成树（Minimum Spanning Tree, MST）是图论中的一个重要概念，它在图论中具有广泛的应用和重要的理论价值。

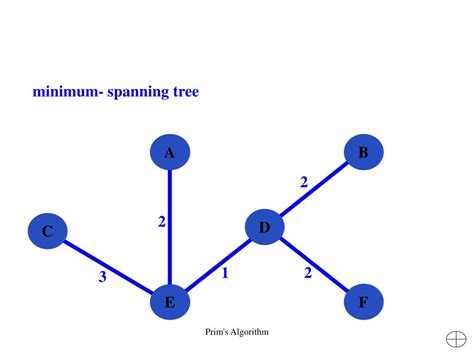
定义

最小生成树（MST）是图论中的一个核心概念，它定义为在一个无向连通加权图中，包含图中所有顶点的子图，且边的权值之和最小的树。具体来说，MST 是一个生成树（即包含图中所有顶点的无环连通子图），并且其边的总权重在所有可能的生成树中是最小的。

特性

• 包含所有顶点：MST 必须包含图中的所有顶点。
• 无环：MST 是一棵树，因此它不包含任何环路。
• 最小权重：MST 的边的总权重在所有可能的生成树中是最小的。
• 边数：对于一个有  个顶点的图，MST 的边数为 。

算法

求解最小生成树的常用算法包括：

• 克鲁斯卡尔算法（Kruskal's Algorithm） ：该算法通过按边的权重从小到大排序，依次选择不形成环的边来构建 MST。它使用并查集（Union-Find）来检测环的形成。
• 普里姆算法（Prim's Algorithm） ：该算法从一个起始顶点开始，逐步扩展生成树，每次选择连接已生成树与未生成树的最小边。
• Borůvka 算法：该算法通过迭代合并最小边来构建 MST，是一种早期的 MST 算法。

应用

最小生成树在多个领域有广泛的应用，包括：

• 网络设计：在通信网络、电力网络、交通网络等基础设施建设中，MST 可以找到最经济的连接方式，即总线路长度最短或总建设成本最低。
• 优化问题：MST 可用于近似旅行商问题、多终端最小割问题、最小成本加权完美聚类分析等。
• 其他领域：MST 在图像处理、生物学、社交网络分析、电路设计等领域也有应用。

总结

最小生成树（MST）是图论中的一个重要概念，它不仅在理论上有重要意义，而且在实际应用中也有广泛的用途。通过克鲁斯卡尔算法和普里姆算法等经典算法，可以有效地求解最小生成树问题，为各种优化问题提供了有效的解决方案