什么是最小二乘法（Ordinary Least Squares, OLS）

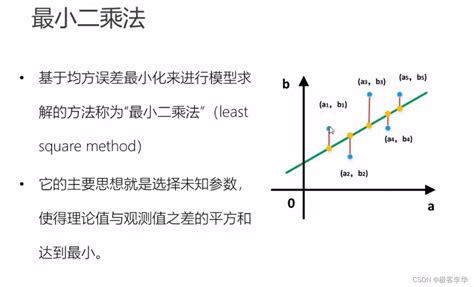
最小二乘法（Ordinary Least Squares, OLS）是一种广泛应用于统计学、经济学、数据科学和机器学习中的回归分析方法。其核心思想是通过最小化观测值与模型预测值之间的平方差之和，来估计模型参数，从而找到最佳拟合线或超平面。

核心思想与原理

最小二乘法的核心思想是通过最小化残差平方和（Residual Sum of Squares, RSS）来估计模型参数。最小二乘法的求解通常通过求解正规方程（Normal Equations）来实现。

假设与局限性

最小二乘法的有效性依赖于一系列假设条件，包括线性关系、独立性、同方差性、正态性、无多重共线性等。如果这些假设被违反，OLS的估计可能变得不准确或无效。例如，当存在多重共线性时，参数估计可能变得不稳定；当存在异方差性时，OLS的估计可能不再是最佳线性无偏估计（BLUE）。

应用与优势

最小二乘法因其简单、高效和直观的特点，被广泛应用于各种领域，包括经济学、金融、医学、社会科学和工程等。它不仅用于建模变量之间的关系，还用于预测和推断因果关系。此外，OLS的结果（如R²、p值、t统计量等）提供了模型拟合度和参数显著性的评估。

实现与工具

最小二乘法的实现通常依赖于统计软件和编程语言，如Python（使用statsmodels、scikit-learn等库）、R、SAS、SPSS等。这些工具提供了便捷的函数和方法，用于数据预处理、模型拟合、结果分析和可视化。

总结

最小二乘法（Ordinary Least Squares, OLS）是一种基础且重要的统计方法，通过最小化残差平方和来估计模型参数，广泛应用于回归分析、预测建模和数据分析。尽管其假设条件较为严格，但其简单性和高效性使其成为统计学和数据科学中的核心工具