什么是最大流算法

最大流算法是解决网络流问题中的核心算法之一，其目标是求解在给定的有向图中，从源点（source）到汇点（sink）的最大流量。最大流问题通常涉及一个网络图，其中包含节点、边和边的容量限制。最大流算法的核心思想是通过不断寻找增广路径（augmenting paths）来增加从源点到汇点的流量，直到无法再增加为止。

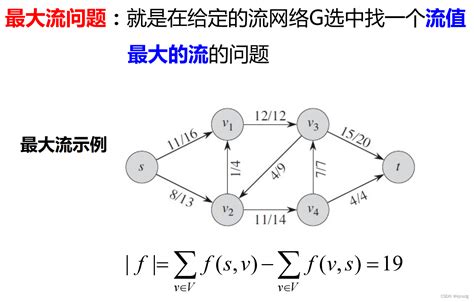
最大流问题的基本概念

最大流问题的目标是找到从源点到汇点的最大流量，同时满足以下条件：

• 每条边的流量不能超过其容量限制。
• 对于每个节点（除了源点和汇点），流入节点的流量等于流出节点的流量。
• 最大流的值等于最小割的容量（最小割最大流定理）。

最大流算法的核心思想

最大流算法的核心思想是通过不断寻找增广路径（augmenting paths）来增加流量。增广路径是指从源点到汇点的一条路径，其中每条边的剩余容量（residual capacity）大于0。通过沿着增广路径增加流量，可以逐步提高总流量。

常见的最大流算法

1. Ford-Fulkerson算法：该算法通过不断寻找增广路径来增加流量，直到无法再增加为止。其时间复杂度为O(Ef)，其中E是边的数量，f是最大流的值。
2. Edmonds-Karp算法：这是Ford-Fulkerson算法的一种改进版本，使用广度优先搜索（BFS）来寻找最短路径，从而提高算法的效率。其时间复杂度为O(VE²)，其中V是顶点的数量，E是边的数量。
3. Dinic算法：该算法通过引入分层图（level graph）的概念，进一步优化了最大流算法的性能，适用于大规模网络流问题。

最大流算法的应用

最大流算法在多个领域有广泛应用，包括交通网络、通信网络、资源分配、图像识别等。例如，在交通网络中，最大流算法可以用于优化交通流量的分配；在通信网络中，可以用于优化数据传输的效率。

总结

最大流算法是一种解决网络流问题的核心算法，通过不断寻找增广路径来增加流量，直到达到最大流。该算法在多个领域有广泛应用，是计算机科学和工程领域的重要工具