什么是按秩合并（Union by Rank）

按秩合并（Union by Rank）是并查集（Disjoint Set Union, DSU）算法中的一种优化策略，旨在减少合并操作时树的高度，从而提高后续查找操作的效率。其核心思想是通过维护一个“秩”（Rank）数组来记录每个集合的树的高度或节点数量的估计值，并在合并两个集合时，将秩较小的树合并到秩较大的树中，以保持树的平衡。

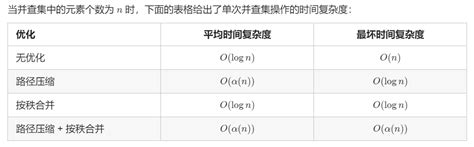
按秩合并的核心原理

1. 秩的定义
   秩（Rank）是一个估计值，用于表示树的高度或节点数量的上界。它并不精确等于树的实际高度，但可以作为树高度的估计值。秩的值通常在合并操作中更新，以反映树的结构变化。
2. 合并策略
   在合并两个集合时，按秩合并的规则是：
   • 如果两个集合的根节点的秩不同，则将秩较小的根节点的父节点指向秩较大的根节点。
   • 如果两个集合的根节点的秩相同，则任选一个作为根节点，并将另一棵树的秩加1（表示树的高度增加）。
3. 目的
   通过这种合并策略，可以避免树的高度过度增长，从而减少后续查找操作的时间复杂度。按秩合并与路径压缩（Path Compression）结合使用时，可以进一步优化并查集的性能。

实现方式

按秩合并的实现通常需要维护一个秩数组（Rank Array），用于记录每个根节点的秩值。在合并操作中，通过比较两个根节点的秩值，决定合并的方向。例如，在代码中，通常会使用以下逻辑：

def union(x, y, parent, rank):
    root_x = find(x, parent)
    root_y = find(y, parent)
    if root_x == root_y:
        return
    if rank[root_x] < rank[root_y]:
        parent[root_x] = root_y
    elif rank[root_x] > rank[root_y]:
        parent[root_y] = root_x
    else:
        parent[root_y] = root_x
        rank[root_x] += 1

优势与效果

• 减少树的高度：通过将较小的树合并到较大的树中，可以避免树的高度过度增长，从而减少查找操作的时间复杂度。
• 提高效率：结合路径压缩，按秩合并可以将并查集的查找和合并操作的时间复杂度优化到接近线性级别。

总结

按秩合并是一种高效的优化策略，通过维护秩值和合理的合并策略，可以显著提升并查集的性能。它在实际应用中广泛用于需要高效处理动态集合合并和查找的场景，如图论、算法竞赛和数据库管理等领域