什么是广度优先搜索（Breadth-First Search，简称BFS）

广度优先搜索（Breadth-First Search，简称BFS）是一种用于遍历或搜索图、树等数据结构的算法。其核心思想是按照层级顺序访问节点，即优先访问与起始节点距离较近的节点，然后再访问更远的节点。这种搜索方式通常使用队列来实现，因为队列具有先进先出（FIFO）的特性，能够保证节点按层次顺序被访问。

BFS的基本原理

1. 起始点选择：从一个指定的起始节点开始搜索。
2. 队列初始化：将起始节点加入一个空队列中，并将其标记为已访问。
3. 逐层扩展：
   • 从队列中取出一个节点，访问其所有未被访问过的邻接节点。
   • 将这些邻接节点标记为已访问，并将它们加入队列。
   • 重复上述过程，直到队列为空或找到目标节点为止。
4. 时间复杂度：BFS的时间复杂度为O(V+E)，其中V是顶点数，E是边数。这是因为每个顶点和每条边都会被访问一次。

BFS的特点

1. 按层次访问：BFS会优先访问与起始节点距离较近的节点，然后逐步扩展到更远的节点。这使得BFS特别适用于寻找最短路径问题。
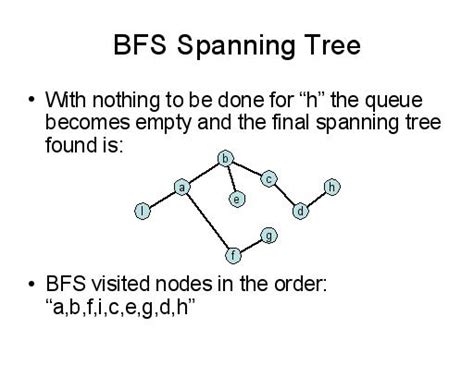
2. 生成树结构：在遍历过程中，BFS会生成一棵以起始节点为根的广度优先树（BFS树），包含所有可达的节点。
3. 避免重复访问：通过标记已访问的节点，BFS可以避免重复访问，从而提高效率。

BFS Spanning Tree

BFS的应用场景

1. 寻找最短路径：在无权图中，BFS可以找到从起点到其他所有节点的最短路径。这是因为BFS按层次扩展，确保了路径长度最小。
2. 图的连通性判断：通过BFS可以判断图是否连通，即所有节点是否可以通过边相互到达。
3. 网络分析：在社交网络中，BFS可以用来计算用户之间的最短关系链。
4. 迷宫问题：BFS可以用来解决迷宫问题，找到从起点到终点的最短路径。

BFS的实现

1. 数据结构：使用队列来存储待访问的节点。
2. 状态标记：通常使用三种颜色（白色、灰色、黑色）来标记节点的状态：
   • 白色：未访问。
   • 灰色：正在访问。
   • 黑色：已完全访问。
3. 伪代码：

   visited = set()  # 存储已访问的节点
   queue = deque([start_node])  # 初始化队列

   while queue:
       node = queue.popleft()
       if node not in visited:
           visited.add(node)
           for neighbor in get_neighbors(node):
               if neighbor not in visited:
                   queue.append(neighbor)

图的遍历算法：广度优先搜索和深度优先搜索…

BFS与DFS的区别

• 搜索方式：BFS按层次扩展，而DFS深入到树的深处再回溯。
• 适用场景：BFS适用于寻找最短路径和连通性问题；DFS适用于深度优先搜索的问题，如二叉树遍历。
• 空间复杂度：BFS的空间复杂度为O(V)，而DFS的空间复杂度为O(D)，其中D是树的最大深度。

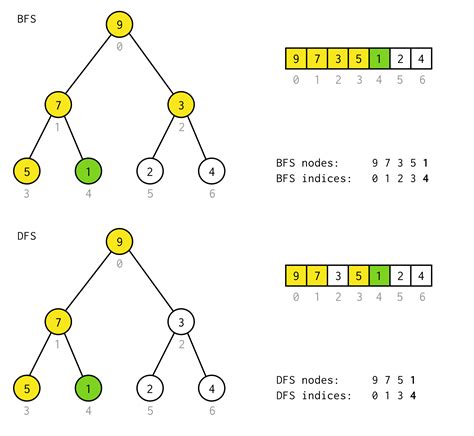
Compare Bfs And Dfs / 12 BFS vs DFS Artificial Intelligence En…

广度优先搜索是一种简单但非常强大的算法，广泛应用于图论、网络分析和人工智能等领域。它通过系统地按层次访问节点，能够高效地解决许多实际问题。