什么是余弦相似度（Cosine Similarity）

余弦相似度（Cosine Similarity）是一种用于衡量两个向量之间相似性的指标，其核心思想是通过计算两个向量之间夹角的余弦值来评估它们的相似性。以下是关于余弦相似度的详细解释：

1. 定义与数学公式

2. 核心思想

余弦相似度的核心思想是关注向量的方向而非大小。它不考虑向量的长度或模长，只关注向量之间的方向相似性。因此，即使两个向量的长度不同，只要它们的方向相似，余弦相似度也会较高。这一特性使得余弦相似度在处理高维数据、稀疏数据时具有优势。

3. 应用场景

余弦相似度广泛应用于多个领域，包括：

• 文本分析：在自然语言处理中，将文本表示为向量，通过余弦相似度计算文本之间的相似性，用于文档检索、推荐系统、抄袭检测等。
• 推荐系统：根据用户偏好或物品特征的相似性进行推荐。
• 信息检索：在搜索引擎中，通过计算查询与文档的余弦相似度来排序结果。
• 图像识别：在图像处理中，通过计算图像特征向量的余弦相似度来识别相似图像。
• 生物信息学：在DNA序列分析中，用于比较序列的相似性。

4. 计算方法与实现

余弦相似度的计算可以通过多种方式实现：

• 手动计算：通过公式 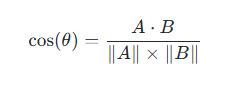 计算；
• 编程库：使用Python中的NumPy、SciPy、TensorFlow等库中的函数进行高效计算。
• 数据库支持：在数据库系统中，如TiDB、腾讯云向量数据库等，支持通过内置函数或索引加速余弦相似度的计算。

5. 优势与局限性

• 优势：
  • 对向量长度不敏感，仅关注方向相似性；
  • 适用于高维数据和稀疏数据；
  • 计算效率高，适合大规模数据处理。
• 局限性：
  • 无法直接处理零向量（当向量为零时，余弦相似度为2.0，需特殊处理）；
  • 无法直接反映向量的绝对相似性，仅反映方向相似性。

6. 总结

余弦相似度是一种简单而强大的相似性度量方法，广泛应用于数据科学、自然语言处理、推荐系统等领域。它通过计算向量之间的夹角余弦值，能够有效衡量向量之间的方向相似性，尤其适用于处理高维和稀疏数据。尽管存在一些局限性，但其在实际应用中具有广泛的适用性和高效性