什么是二叉堆

二叉堆是一种特殊的数据结构，它基于二叉树的结构，具有特定的性质和操作。

1. 二叉堆的定义

二叉堆是一种特殊的二叉树，通常称为完全二叉树。它具有以下特点：

• 每个节点最多有两个子节点（左子节点和右子节点）。
• 二叉堆分为两种类型：最大堆和最小堆。
  • 最大堆：每个节点的值大于或等于其子节点的值。
  • 最小堆：每个节点的值小于或等于其子节点的值。
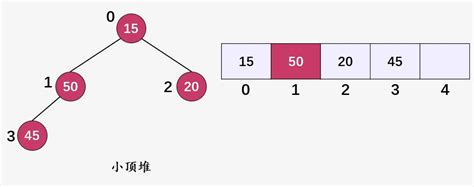
• 二叉堆通常用数组表示，根节点位于数组的起始位置，左子节点和右子节点的索引可以通过公式计算（例如，左子节点为 2*i+1，右子节点为 2*i+2）。

2. 二叉堆的性质

• 二叉堆的结构是完全二叉树，即除了最后一层外，所有层都被完全填满，且最后一层的节点尽可能靠左排列。
• 二叉堆的节点值满足特定的顺序关系，即父节点的值大于或小于其子节点的值，具体取决于最大堆或最小堆的定义。

3. 二叉堆的操作

二叉堆支持多种基本操作，包括：

• 插入操作：将新元素插入到堆中，并通过“上浮”操作调整堆的结构，以维持堆的性质。
• 删除操作：删除堆顶元素（最大值或最小值），并进行“下沉”操作以维持堆的性质。
• 获取堆顶元素：返回堆顶元素的值，时间复杂度为 O(1)。
• 构建堆：将一个无序数组转换为堆，时间复杂度为 O(n) 。

4. 二叉堆的应用

二叉堆广泛应用于以下场景：

• 优先队列：二叉堆是实现优先队列的核心数据结构，支持高效地获取最大值或最小值。
• 堆排序：堆排序是一种基于二叉堆的排序算法，时间复杂度为 O(n log n) 。
• 其他应用：如合并有序数组、查找第 K 大元素、优化算法等。

5. 二叉堆的实现

二叉堆通常通过数组实现，利用数组的索引关系来表示树的结构。例如，父节点的索引为 i，左子节点的索引为 2*i+1，右子节点的索引为 2*i+2。

总结

二叉堆是一种高效的数据结构，结合了二叉树的结构和特定的顺序性质，广泛应用于优先队列、排序和优化算法等领域。其核心特性包括完全二叉树的结构、最大堆或最小堆的性质以及高效的插入、删除和查询操作